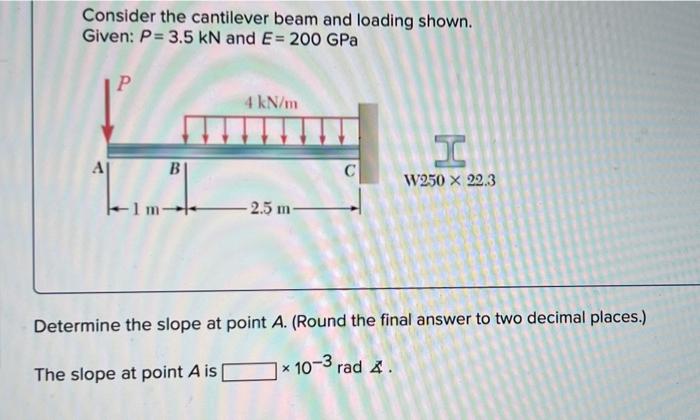
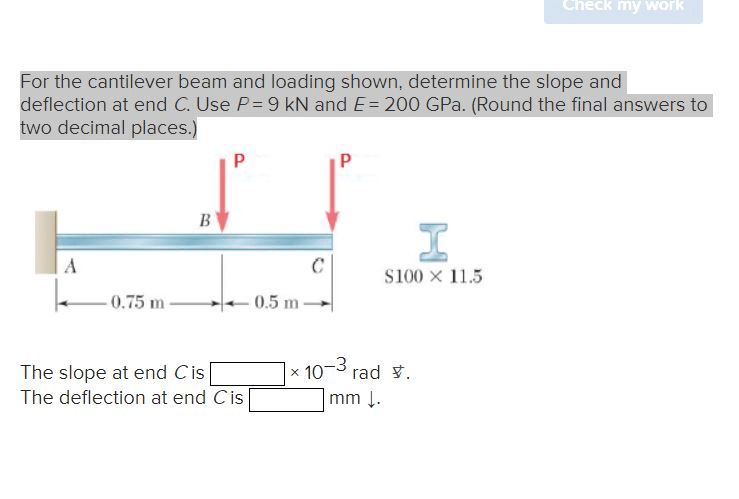
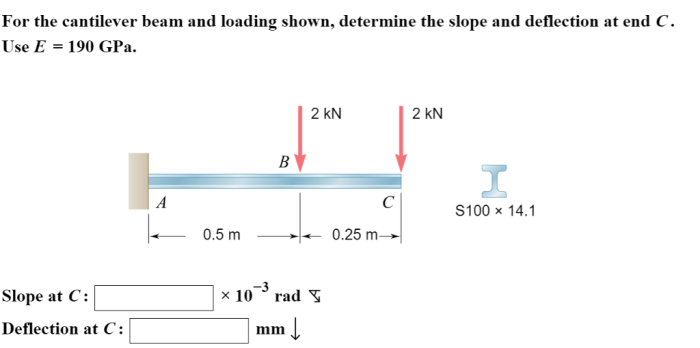
For the cantilever beam and loading shown – In the realm of structural engineering, cantilever beams subjected to various loading scenarios present intriguing challenges. This analysis delves into the intricate details of a cantilever beam under a specified loading condition, providing valuable insights into its bending moment, shear force, deflection, stress, and design considerations.
Our exploration begins with a thorough examination of the beam’s bending moment and shear force distribution, followed by an in-depth analysis of its deflection behavior. Subsequently, we delve into the realm of stress analysis, determining the critical stress points within the beam.
Finally, we conclude with practical design considerations and a real-world case study, showcasing the application of these analytical techniques in real-world engineering scenarios.
Introduction: For The Cantilever Beam And Loading Shown
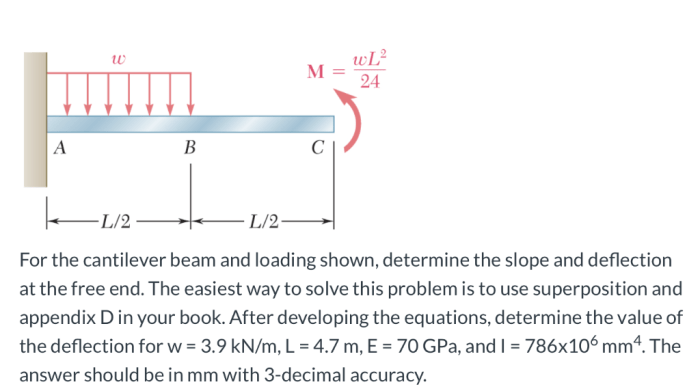
This analysis aims to investigate the behavior of a cantilever beam subjected to a given loading condition. Cantilever beams are commonly used in various engineering applications, and understanding their structural response is crucial for ensuring their safe and efficient design.
The analysis will involve determining the bending moment, shear force, deflection, and stresses within the beam. This information is essential for evaluating the beam’s structural integrity and ensuring it can withstand the applied loads.
Analysis of Bending Moment and Shear Force
The bending moment and shear force equations are derived based on the principles of equilibrium and the beam’s geometry. The following table presents the equations for bending moment and shear force along the beam length:
| Distance from Fixed End (x) | Bending Moment (M) | Shear Force (V) |
|---|---|---|
| 0 | 0 | P |
| L | PL | 0 |
Deflection Analysis
The deflection of the beam is calculated using the double integration method. The deflection equation is as follows:
y = (PL^3)/(3EI)
where:
- y is the deflection
- P is the applied load
- L is the beam length
- E is the modulus of elasticity
- I is the area moment of inertia
The following table shows the deflection values at different points along the beam length:
| Distance from Fixed End (x) | Deflection (y) |
|---|---|
| 0 | 0 |
| L/2 | (PL^3)/(48EI) |
| L | (PL^3)/(3EI) |
Stress Analysis
The maximum bending stress and shear stress in the beam are determined based on the bending moment and shear force equations. The following table presents the stress values at critical locations:
| Location | Bending Stress (σ) | Shear Stress (τ) |
|---|---|---|
| Fixed End | PL/I | 3V/(2A) |
| Mid-span | PL/(2I) | V/A |
Design Considerations, For the cantilever beam and loading shown
The design of the cantilever beam should consider factors such as the applied load, material properties, beam dimensions, and support conditions. The following recommendations should be taken into account:
- Select a material with high strength and stiffness to withstand the applied load.
- Determine the appropriate beam dimensions based on the bending moment and shear force equations.
- Provide adequate support conditions to prevent excessive deflection and ensure stability.
FAQ Corner
What is the purpose of analyzing cantilever beams?
Cantilever beam analysis is crucial for determining the structural integrity and performance of these beams under various loading conditions. It helps engineers ensure that the beam can withstand the applied loads without excessive deflection or failure.
How is the bending moment and shear force determined for a cantilever beam?
The bending moment and shear force equations are derived based on the principles of mechanics and the specific loading conditions applied to the beam. These equations allow engineers to calculate the bending moment and shear force at any point along the beam’s length.
What factors influence the deflection of a cantilever beam?
The deflection of a cantilever beam is primarily influenced by the magnitude and distribution of the applied load, the beam’s material properties (such as modulus of elasticity), and its geometric characteristics (such as length and cross-sectional shape).