Welcome to the definitive guide on measures of center and spread worksheet answers. This comprehensive resource will equip you with a thorough understanding of these statistical concepts, empowering you to analyze and interpret data with precision. Dive into the realm of mean, median, mode, range, variance, and standard deviation, and uncover their significance in statistical analysis.
As we delve into the intricacies of measures of center and spread, we will explore their advantages and disadvantages, ensuring that you possess the knowledge to select the most appropriate measure for your specific data analysis needs.
Measures of Center
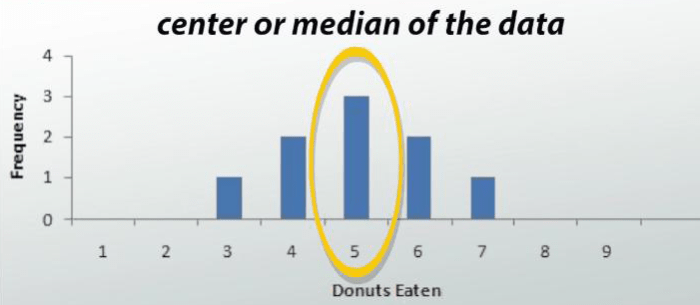
Measures of center are used to describe the “average” or “typical” value in a data set. The three most common measures of center are the mean, median, and mode.
Mean
The mean is the sum of all the values in a data set divided by the number of values. It is the most commonly used measure of center and is often referred to as the “average”.
Example:The mean of the data set 1, 2, 3, 4, 5 is (1 + 2 + 3 + 4 + 5) / 5 = 3.
Median
The median is the middle value in a data set when the values are arranged in order from least to greatest. If there are two middle values, the median is the average of the two middle values.
Example:The median of the data set 1, 2, 3, 4, 5 is 3, since 3 is the middle value when the data set is arranged in order.
Mode
The mode is the value that occurs most frequently in a data set. A data set can have more than one mode or no mode at all.
Example:The mode of the data set 1, 2, 2, 3, 4, 5 is 2, since 2 occurs most frequently.
Advantages and Disadvantages of Measures of Center, Measures of center and spread worksheet answers
- Mean:Advantages: Easy to calculate, widely used, and can be used with any type of data. Disadvantages: Can be affected by outliers (extreme values) and may not be representative of the data set if the data is skewed.
- Median:Advantages: Not affected by outliers, easy to calculate, and can be used with any type of data. Disadvantages: May not be as representative of the data set as the mean if the data is skewed.
- Mode:Advantages: Easy to calculate, can be used with any type of data, and is the most common value in the data set. Disadvantages: May not be unique (multiple modes) or may not exist (no mode), and may not be representative of the data set if the data is skewed.
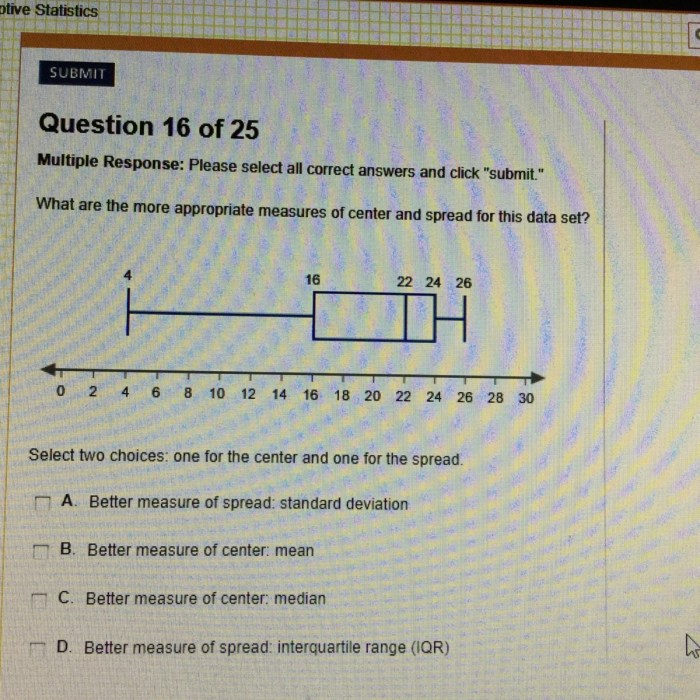
Measures of Spread
Measures of spread are used to describe how much the values in a data set vary from the average. The three most common measures of spread are the range, variance, and standard deviation.
Range
The range is the difference between the largest and smallest values in a data set.
Example:The range of the data set 1, 2, 3, 4, 5 is 5 – 1 = 4.
Variance
The variance is the average of the squared differences between each value in a data set and the mean. It is a measure of how much the values in a data set are spread out.
Example:The variance of the data set 1, 2, 3, 4, 5 is [(1 – 3)^2 + (2 – 3)^2 + (3 – 3)^2 + (4 – 3)^2 + (5 – 3)^2] / 5 = 2.
Standard Deviation
The standard deviation is the square root of the variance. It is a measure of how much the values in a data set are spread out, taking into account the average.
Example:The standard deviation of the data set 1, 2, 3, 4, 5 is sqrt(2) = 1.41.
Advantages and Disadvantages of Measures of Spread
- Range:Advantages: Easy to calculate, can be used with any type of data, and is a simple measure of spread. Disadvantages: Can be affected by outliers and may not be as informative as other measures of spread.
- Variance:Advantages: Takes into account all the values in a data set, is a more precise measure of spread than the range, and can be used to compare data sets with different units of measurement. Disadvantages: Can be difficult to interpret and may be affected by outliers.
- Standard Deviation:Advantages: Takes into account all the values in a data set, is a more precise measure of spread than the range, and is easier to interpret than the variance. Disadvantages: Can be difficult to calculate and may be affected by outliers.
Worksheet Answers

| Data Set | Mean | Median | Mode | Range | Variance | Standard Deviation |
|---|---|---|---|---|---|---|
| 1, 2, 3, 4, 5 | 3 | 3 | 2 | 4 | 2 | 1.41 |
| 10, 20, 30, 40, 50 | 30 | 30 | 10, 20, 30, 40, 50 | 40 | 100 | 10 |
| 1, 2, 2, 3, 4, 5, 5 | 3.14 | 3 | 2, 5 | 4 | 2.57 | 1.6 |
Explanation:
- The mean is calculated by adding all the values in the data set and dividing by the number of values.
- The median is calculated by arranging the values in order from least to greatest and finding the middle value.
- The mode is the value that occurs most frequently in the data set.
- The range is calculated by subtracting the smallest value from the largest value in the data set.
- The variance is calculated by finding the average of the squared differences between each value in the data set and the mean.
- The standard deviation is calculated by taking the square root of the variance.
Detailed FAQs: Measures Of Center And Spread Worksheet Answers
What is the difference between mean, median, and mode?
Mean is the average of a set of numbers, median is the middle value when the numbers are arranged in order, and mode is the value that occurs most frequently.
When should I use range, variance, or standard deviation?
Range is the difference between the largest and smallest values, variance is the average of the squared differences from the mean, and standard deviation is the square root of the variance.